B-Tree
BST Performance
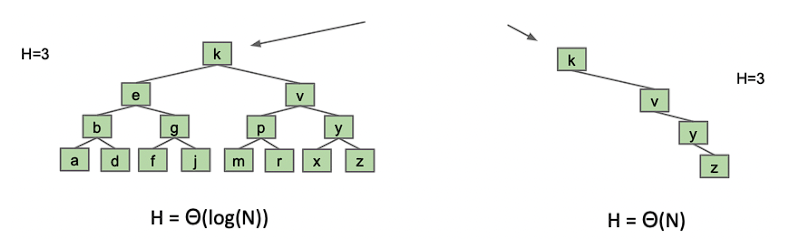
Binary Search Tree 根据插入的数据不同,最好的情况树的高度为 $O(logN)$, 最坏的情况为 $O(N)$。
17.3 B-Tree Operations
Avoiding Imbalance
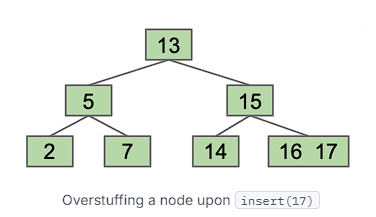
采用的一种方法是“过度填充”叶节点。我们不需要在插入时添加新节点,而是简单地将新值堆叠到适当位置的现有叶节点中。
Moving Items Up
为了改善过度填充叶节点的问题,我们可以考虑在叶节点达到一定数量的值时“上移”一个值。
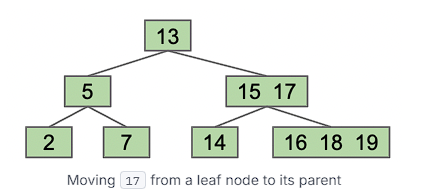
然而,这遇到了一个问题,我们的二分搜索属性不再被保留——16 在 17 的右边。这时候我们需要将过度填充节点的子节点划分:
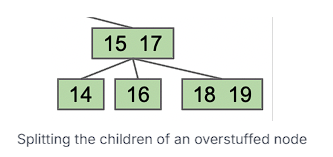
在这个结构上的搜索操作将与 BST 完全相同,除了值在 15 到 17 之间,我们去中间的子节点,而不是左边或右边。
如果我们设置一个常数𝐿作为节点大小的限制,那么我们的搜索时间只会增加一个常数因子。
添加到节点可能会导致级联链式反应,如下图所示,我们添加了 25 和 26。
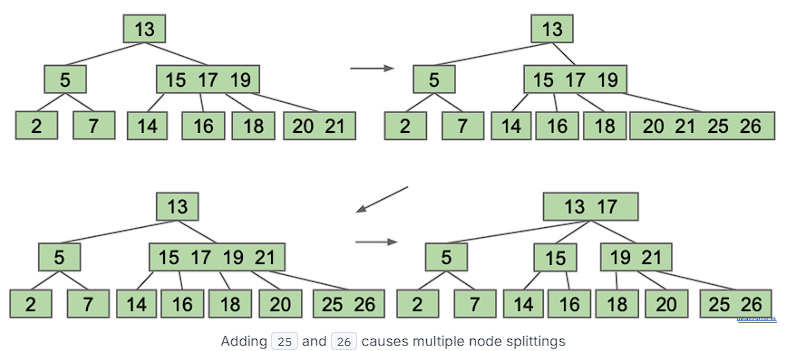
当我们的根超过限制,我们需要增加树的高度:
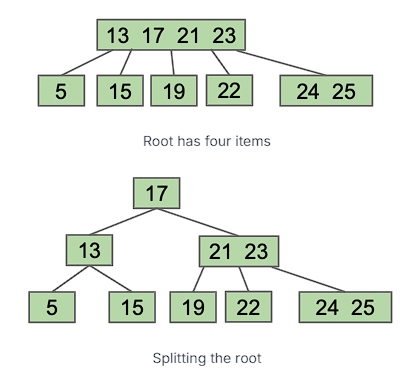
这种数据结构的名称为 B-Tree, 如果每个节点最多有 3 个 items, 那么我们称之为 2-3-4 trees 或者 2-4 trees(一个 node 可以有 2/3/4 个子节点)。如果每个节点最多有 2 个 items,那么称之为 2-3 trees。
17.4 B-Tree Invariants
- 所有叶子节点到根节点的距离都是一样的。
- 具有 k 项的非叶节点必须恰好有 k + 1 个子节点。
17.5 B-Tree Performance
根据每个节点最多包含 $L$ 个 items, B-Tree 的最大高度在 $log_{L+1}N$ 到 $log_2N$ 之间。
overall height 仍然是 $O(logN)$。
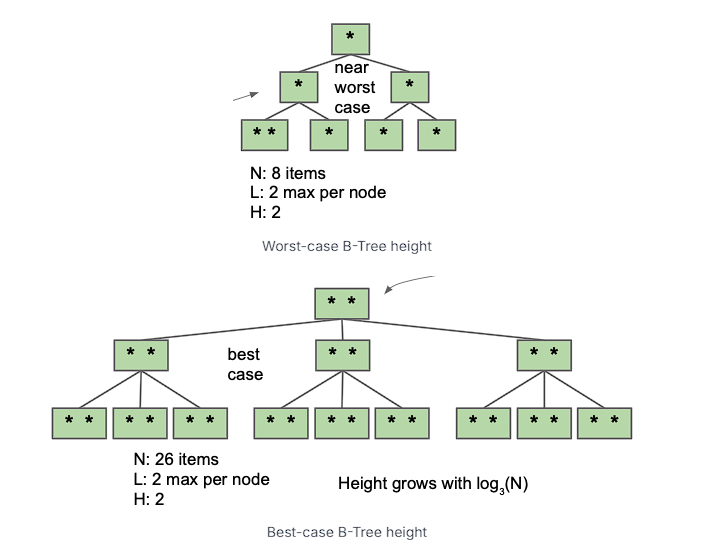
Runtime for contains
最坏的情况我们需要检查 node 中的 L 个 item, 这时 contains 的时间复杂度为$O(LlogN)$, 因为 L 是常数可以省略,所以 contains 的时间复杂度为$O(logN)$。
Runtime for add
最坏的情况我们需要拆分叶节点,因为树的高度为 $O(logN)$, 所以我们最坏需要做 $O(logN)$ 次拆分。
这只给我们的运行时间增加了 $O(logN)$, 因此 add 的时间复杂度仍然为 $O(logN)$。