Asymptotics

15.1 For Loops

int N = A.length;
for (int i = 0; i < N; i += 1)
   for (int j = i + 1; j < N; j += 1)
      if (A[i] == A[j])
         return true;
return false;

有两种方法来渐进分析：

Methood 1: 计算运算符的数量

比如看==的执行次数，第一次循环为$N-1$次，第二次为$N-2$次，…，最后一次为$1$次，所以总共为$1+2+3+…+N-1$，即$N(N-1)/2$, 运行时间为 $\theta(N^2)$。

Methood 2: 几何分析

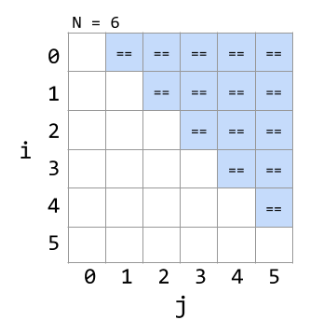
可以看到==的执行次数和三角形的两边 $N-1$ 都有关系，所以面积 in $N^2$ family, 可以得到运行时间为 $\theta(N^2)$


再看一个例子：

public static void printParty(int N) {
   for (int i = 1; i <= N; i = i * 2) {
      for (int j = 0; j < i; j += 1) {
         System.out.println("hello");   
         int ZUG = 1 + 1;
      }
   }
}

执行次数为 $1+2+4+…+N$, 和为 $2N-1$

所以执行时间为 $\theta(N)$


总结两条规律：

$1+2+3+…+Q=Q(Q+1)/2=Θ(Q​2​​)$

$1+2+4+8+…+Q=2Q−1=Θ(Q)$

15.2 Recursion

public static int f3(int n) {
   if (n <= 1) 
      return 1;
   return f3(n-1) + f3(n-1);
}

执行次数为 $1+2+4+…+2^N$, 和为 $2^N-1$

二分查找的时间复杂度是 $log(N)$

15.4 Mergesort

归并排序的时间复杂度是 $N * log(N)$

每一层都需要 $N$ 次排序，共有 $log_{2}N$ 层。

  • The top level takes ~N AU.
  • Next level takes ~N/2 + ~N/2 = ~N.
  • One more level down: ~N/4 + ~N/4 + ~N/4 + ~N/4 = ~N.

Thus, total runtime is ~Nk, where k is the number of levels.

How many levels are there? We split the array until it is length 1, so k = $log_{2}N$, Thus the overall runtime is $Θ(N∗log(N))$